深度学习中的优化器_羽林娱乐教育培训留学机构

深度学习中的优化器

新闻资讯 | 2024-08-26 05:09

1.优化器的重要性

神经网络的参数巨多，需要合适的算法来进行参数的学习，也就是优化器。可以说，优化器是神经网络的眼睛，是神经网络蓬勃发展的基础。现在的优化器基本都是梯度下降法，本文主要介绍梯度下降法。也可以是梯度上升，就看目标函数是要求max还是min。至于二阶的，比如牛顿算法，计算量太大，实际价值不高。

2.优化器详解

所有要训练的参数记为 $\ heta$ ,目标函数为 $J(\ heta)$ ,考虑最小化目标函数，要用梯度下降法。梯度为 $\ riangle _{\ heta}J(\ heta)$ 。梯度是函数变化最快的方向，如果函数是凸函数，那么梯度相反的方向就是目标函数更小的方向，梯度下降就是在这个方向上快速的向最小点移动。通常都会有一个步长 $\\eta$ 来控制下降的快慢。

神经网络中的目标函数并不是凸函数，所以梯度下降很有可能就困在局部最小或者鞍点，因为此时，梯度很小，无法更新。好的优化器是会考虑这些，想办法从鞍点跳出的。

2.1 Batch Gradient Descent梯度下降

这是最原始的方式，将所有的训练数据得到的损失，一起计算梯度下降值进行更新参数。基本形式为 $\ heta=\ heta - \\eta \ riangle_{\ heta}J(\ heta)$ .由于每次迭代需要遍历所有训练集，所以，它不适用于在线更新模型。当训练集太大时，这种方式极其慢。其伪码如下：

for i in range(epochs):
    params_grad=evaluate_gradient(loss_function,data,params)
    params=params - learning_rate * params_grad

2.2 Stochastic Gradient Descent随机梯度下降

Batch Gradient Descent（SGD）每次需要遍历全部训练集，速度太慢，那么SGD，每次只用一个样本进行计算梯度，参数更新。其形式为 $\ heta=\ heta - \\eta \ riangle_{\ heta}J(\ heta,x^{i},y^{i})$ 。Batch Gradient Descent计算时有些相近的训练样本，都要进行计算，是有重复计算的，而采用SGD，可以避免这一类的重复计算。但是SGD的问题在于波动太大。波动太大的结果是有可能跳出鞍点，但是收敛太慢。直观感受请看

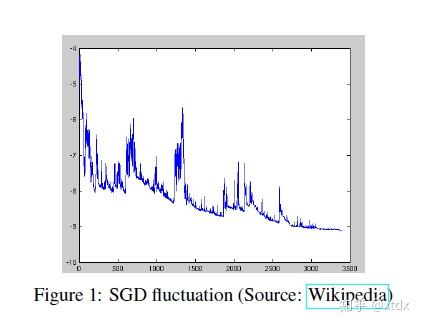
实际中，可以设定一些参数，让步长随着训练的进行而减小。其伪码如下：

for i in range(nb_epochs):
    shuffle(data)
    for example in data :
        params_grad=evaluate_gradient(loss_function , example , params)
        params=params - learning_rate * params_grad

2.3 mini-batch Gradient Descent

Batch gradient descent和SGD都太极端了，完全可以采用折中的方式，那么mini-batch梯度下降就是。每次在一个mini-batch的训练数据上进行梯度计算，参数更新。这样，既不会每次计算量太大，也不会收敛太慢。其形式为 $\ heta=\ heta - \\eta \ riangle_{\ heta}J(\ heta,x^{i:i+n},y^{i:i+n})$ .对于mini-batch的选择取决于显卡的大小，一般取8~256都可以。

其伪码如下：

for i in range (nb_epochs):
    shuffle(data)
    for batch in get_batches(data , batch_size):
        params_grad=evaluate_gradient(loss_function , batch , params)
        params=params - learning_rate * params_grad

要了解其他的优化器，需要了解mini-batch的几个缺点：

1）对步长比较敏感，步长的选择直接决定了最终的性能。如果步长太大，可能不收敛，如果步长太小，更新太慢。虽然可以选择一些方式随着训练进行步长的修改，但是需要人为设定和干预。

2）对不同的参数采用了相同的步长，我们希望的是对出现频率较高的参数，步长小点，频率低的，步长大点，暂时无法做到。

3）可能在鞍点无法跳出。

2.4 Momentum

SGD在目标函数的局部最优点（比如，某一维变化快）会反复震荡，也就是对某个下降路径没有信心。为了解决这个问题，可以采用Momentum.这是物理中动量的概念。参数更新不只是依赖于当前的梯度，也依赖于过去的梯度。其形式为：

$\\begin{align}&v_{t}=\\gamma v_{t-1}+ \\eta \ riangle_{\ heta}J(\ heta)\\\\ &\ heta_{t}=\ heta_{t-1}-v_{t}\\end{align}$

$\\gamma$ 一般取0.9左右。对Momentum的感性认识是，如果两次方向一样，则会增强，如果不一致，则减弱。其与SGD的对比：

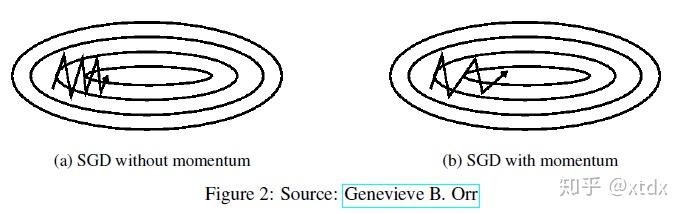
2.5 Nesterov accelerated gradient(NAG)或者Nesterov

Nesterov是在Momentum的基础上进行的改进，基本思路是计算梯度的时候预估参数下一个可能的值，估计时也用到了前一个时刻的动量 $v_{t-1}$ ，即将 $\ riangle_{\ heta}J(\ heta)$ 变为 $\ riangle_{\ heta}J(\ heta-\\gamma v_{t-1})$ .所以，其形式为：

$\\begin{align}&v_{t}=\\gamma v_{t-1}+ \\eta \ riangle_{\ heta}J(\ heta- \\gamma v_{t-1})\\\\ &\ heta_{t}=\ heta_{t-1}-v_{t}\\end{align}$ , $\\gamma$ 依然是0.9左右。

2.6 Adagrad

之前提到的SGD的缺点之一是对所有的参数以同样的步长去更新，这样对出现频率不一样的参数其实是不好的。Adagrad就是要解决这个问题。t时刻第i个参数的梯度记为 $g_{t,i}=\ riangle_{\ heta}J(\ heta_{t,i})$ ,对第i个参数的Adagrad的形式为： $\ heta_{t,i}=\ heta_{t-1,i}-\\frac{\\eta}{\\sqrt{G_{t-1,ii}+\\epsilon}}g_{t-1,i}$ ,其中 $G_{t-1,ii}$ 表示前t-1时刻，第i个梯度的平方和， $\\epsilon$ 是一个很小的值，防止分母为0。很神奇的是，不加sqrt,效果很差。

由以上介绍可以看到，对所有参数来说，Adagrad的形式为 $\ heta_{t}=\ heta_{t-1}-\\frac{\\eta}{\\sqrt{G_{t-1}+\\epsilon}}\\odot g_{t-1}$ ，一般 $\\eta$ 设置为0.1,随着训练的进行，会逐渐减小。

2.7 Adadelta

Adadelta是对Adagrad的改进，因为Adagrad的更新策略还是有些激进，距离太远的时刻的梯度值作用不是很大，所以，Adadelta只考虑某个窗口之内的梯度。但是要保存窗口长度的梯度比较麻烦，于是，实际上采用过去累积值和当前梯度进行加权的方式，即 $E[g^{2}]_{t}=\\gamma E[g^{2}]_{t-1}+(1-\\gamma)g(t)^{2}$ , $\\gamma$ 取值为0.9左右。

根据Adagrad的形式，可以得到Adadelta的形式为： $\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{E[g^{2}]_{t}+\\epsilon}}\\odot g_{t}=\ heta_{t}-\\frac{\\eta}{RMS([g]_{t})}\\odot g_{t}$ .

这个形式其实也可以用，RMSprop就是这样用的。但是，有些研究者认为这个更新规则与实际参数更新还是不一致，于是 $RMS([g]_{t})$ 替换为参数值的插值，即 $RMS[\ riangle \ heta]_{t}=\\sqrt{E[\ riangle \ heta^{2}]_{t}+\\epsilon}=\\sqrt{\\gamma E[\ riangle\ heta^{2}]_{t-1}+(1-\\gamma)\ riangle\ heta_{t}^{2}}$ 。

但是，还有问题，那就是在t时刻更新前，无法计算这个RMS。只能计算一个近似值，最终，可以应用的Adadelta形式为：

$\ heta_{t+1}=\ heta_{t}-\\frac{RMS[\ riangle\ heta]_{t-1}}{RMS[g]_{t}}g(t)$

这样的一个好处是，我们无需给定一个步长。

2.8 RMSprop

在Adadelta中介绍了一种形式，其实就是RMSprop,不同的是，直接给了 $\\gamma$ 值。为什么要单独起个名字呢？因为这是大佬Geoff Hinton在课程里提到的，并没有正式的论文。简单写一下其形式为： $\ heta_{t+1}=\ heta-\\frac{\\eta}{\\sqrt{E[g^{2}]_{t}+\\epsilon}}g_{t}=\ heta-\\frac{\\eta}{\\sqrt{0.9E[g^{2}]_{t-1}+0.1g^{2}_{t}}}g_{t}$ , $\\eta$ 建议0.001.

2.9 Adaptive Moment Estimation(Adam)

Adam应该说在大多数任务上都不错，虽然，有些人认为它更新策略不可理喻。Adam除了像Adadelta那样考虑梯度的平方以外，还考虑了梯度，整体的操作类似。其形式如下：

$\\begin{align}&m_{t}=\\beta_{1}m_{t-1}+(1-\\beta_{1})g_{t}\\\\ &v_{t}=\\beta_{2}v_{t-1}+(1-\\beta_{2})g^{2}_{t}\\\\ &\ ilde{m_{t}}=\\frac{m_{t}}{1-\\beta_{1}^{t}}\\\\ &\ ilde{v_{t}}=\\frac{v_{t}}{1-\\beta_{2}^{t}}\\\\ &\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{\ ilde{v_{t}}+\\epsilon}}\ ilde{m_{t}}\\end{align}$

这里 $\\beta^{t}$ 表示 $\\beta$ 在幂次减小。

2.10 AdaMax

Adamax跟Adam是类似的。首先看Adam的扩展，将 $v_{t}=\\beta_{2}v_{t-1}+(1-\\beta_{2})g^{2}_{t}$ 用 $l_{p}$ norm进行替换得到 $v_{t}=\\beta_{2}^{p}v_{t-1}+(1-\\beta^{p}_{2})|g_{t}|^{p}$ ,理论上，p可以取任意值，但是研究发现太大的值会使训练不稳定，但是用 $l_{\\infty}$ 可以稳定。于是，Adamax就诞生了。 $v_{t}=\\beta_{2}^{\\infty}v_{t-1}+(1-\\beta^{\\infty}_{2})|g_{t}|^{\\infty}=max(\\beta_{2}v_{t-1},|g_{t}|)$ ,最终，Adamax更新形式为：

$\\begin{align}&m_{t}=\\beta_{1}m_{t-1}+(1-\\beta_{1})g_{t}\\\\ &v_{t}=max(\\beta_{2}v_{t-1},|g_{t}|)\\\\ &\ ilde{m_{t}}=\\frac{m_{t}}{1-\\beta_{1}^{t}}\\\\ &\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{v_{t}+\\epsilon}}\ ilde{m_{t}}\\end{align}$

一般来说， $\\eta=0.002,\\beta_{1}=0.9,\\beta_{2}=0.999$

2.11 Nesterov-accelerated Adaptive Moment Estimation(Nadam)

Nadam计算如其名，是Nesterov和Adam的融合。首先，NAG计算时用到了两次前一时刻的动量，一个是计算梯度，一个是计算当前时刻动量，有研究者提出可以只用一次，修改如下：

$\\begin{align}&g_{t}=\ riangle_{\ heta_{t}}J(\ heta_{t})\\\\ &m_{t}=\\gamma m_{t-1}+\\eta g_{t}\\\\ &\ heta_{t+1}=\ heta - (\\gamma m_{t}+\\eta g_{t}) \\end{align}$

在计算梯度时少了前一时刻动量这一项，更新时多了一个梯度项。与NAG并不完全相同，只是考虑的内容一样。

接下来，与Adam融合。 $\ ilde{m_{t}}=\\frac{m_{t}}{1-\\beta_{1}^{t}}=\\frac{\\beta_{1}^{t}m_{t-1}+(1-\\beta_{1}^{t})g_{t}}{1-\\beta_{1}^{t}}$ ,类似改造NAG，用 $m_{t}$ 替换 $m_{t-1}$ ，得到 $\ ilde{m_{t}}=\\beta_{1}^{t+1}\ ilde{m_{t}}+\\frac{(1-\\beta_{1}^{t})g_{t}}{1-\\beta_{1}^{t}}$ ,最终，NAdam的形式为：

$\\begin{align}&m_{t}=\\beta_{1}^{t}m_{t-1}+(1-\\beta_{1}^{t})g_{t}\\\\ &v_{t}=\\beta_{2}^{t}v_{t-1}+(1-\\beta_{2}^{t})g^{2}_{t}\\\\ &\ ilde{m_{t}}=\\frac{m_{t}}{1-\\beta_{1}^{t}}\\\\ &\ ilde{v_{t}}=\\frac{v_{t}}{1-\\beta_{2}^{t}}\\\\ &\ heta_{t+1}=\ heta_{t}-\\frac{\\eta}{\\sqrt{\ ilde{v_{t}}+\\epsilon}}(\\beta_{1}^{t+1}\ ilde{m_{t}}+\\frac{(1-\\beta_{1}^{t})g_{t}}{1-\\beta_{1}^{t}}) \\end{align}$

2.12 Rectified Adam(RAdam)

研究者发现诸如Adam，RMSprop等优化器，都是自适应学习率，这种方式会在训练早期产生较大的方差，所以，这几种方法都采用了warmup，来减小方差。如何选择warmup就是一个技术活，或者看运气。于是，研究者提出了整流器来自适应调节。其形式为：

$\\begin{align}&\\rho_{\\infty}=\\frac{2}{1-\\beta_{2}}- 1\\\\ &g_{t}=\ riangle _{\ heta_{t}}J(\ heta_{t-1})\\\\ &m_{t}=\\beta_{1}m_{t-1}+(1-\\beta_{1})g_{t}\\\\ &v_{t}=\\beta_{2}v_{t-1}+(1-\\beta_{2})g_{t}^{2}\\\\ &\ ilde{m_{t}}=\\frac{m_{t}}{1-\\beta_{1}^{t}}\\\\ &\\rho_{t}=\\rho_{\\infty}-\\frac{2t\\beta_{2}^{t}}{1-\\beta_{2}^{t}}\\\\ &if \\rho_{t}> thes:\\\\ &\\:\\:\\:\\:\\:\\:\ ilde{v_{t}}=\\sqrt{\\frac{v_{t}}{1-\\beta_{2}^{t}}}\\\\ &\\:\\:\\:\\:\\:\\:r_{t}=\\sqrt{\\frac{(\\rho_{t}-4)(\\rho_{t}-2)\\rho_{\\infty}}{(\\rho_{\\infty}-4)(\\rho_{\\infty}-2)\\rho_{t}}}\\\\ &\\:\\:\\:\\:\\:\\:\ heta_{t}=\ heta_{t-1}-\\frac{\\alpha_{t}r_{t}\ ilde{m_{t}}}{\ ilde{v_{t}}}\\\\ &else:\\\\ &\\:\\:\\:\\:\\:\\:\ heta_{t}=\ heta_{t-1}-a_{t}\ ilde{m_{t}}\\end{align}$

3.优化器对比以及如何选择

首先，来一个不同优化器的模拟图

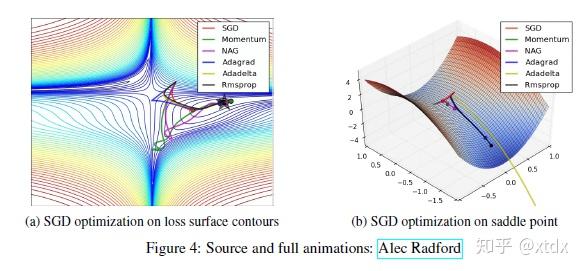
一般来说，自适应学习率的方法，如Adagrad, Adadelta, RMSprop, Adam会更快的收敛，更稳定。SGD, Momentum, NAG比较难以跳出鞍点，但是，跳出鞍点后他们可以找到更优点。

如何选择优化器呢？简单的原则：如果数据稀疏，最好用自适应学习率的方法，Adagrad, Adadelta, RMSprop, Adam。这几个中，优先考虑Adam。至于RAdam是新出的，是否在大多数任务上有效也不一定，最好是尝试一下。在使用Adam等训练一定epoch后，可以换成mini-batch Gradient Descent.